### Floating Point Numbers
You can think of floating point numbe...
Completed in 1951, the *Whirlwind I* was a Cold War-era vacuum tube...
The **Newton-Ralphson** method is an iterative root-finding algorit...
There are a few reasons why the **Newton-Ralphson** method can fail...
This trend mostly continued until today:
 was the first computer to...
To Fernando J. Corbato
for his work in organizing the
concepts and leading the development
of the general-purpose large-scale
time-sharing and resource-sharing
computer systems CTSS and MULTICS
T
ii
" i
FERNANDO J. eORBAT6
I
t is an honor and a pleasure to
accept the Alan Turing
Award. My own work has
been on computer systems,
and that will be my theme.
The essence of systems is that
they are integrating efforts, requir-
ing broad knowledge of the prob-
lem area to be addressed, and the
detailed knowledge required is
rarely held by one person. Thus the
work of systems is usually done by
teams. Hence I am accepting this
award on behalf of the many with
whom I have worked as much as for
myself. It is not practical to name all
the individuals who contributed.
Nevertheless, I would like to give
special mention to Marjorie Dag-
gett and Bob Daley for their parts
in the birth of CTSS and to Bob
Fano and the late Ted Glaser for
their critical contributions to the
development of the Multics System.
Let me turn now to the title of
this talk: "On Building Systems
That Will Fail." Of course the title I
chose was a teaser. I considered and
discarded some alternate titles: "On
Building Messy Systems," but it
seemed too frivolous and suggests
there is no systematic approach.
"On Mastering System Complexity"
sounded like I have all the answers.
The title that came closest, "On
Building Systems that are likely to
have Failures" did not have the
nuance of inevitability that I
wanted to suggest.
What I am really trying to ad-
dress is the class of systems that for
want of a better phrase, I will call
"ambitious systems." It almost goes
without saying that ambitious sys-
tems never quite work as expected.
Things usually go wrong--
sometimes in dramatic ways. And
this leads me to my main thesis,
namely, that the question to ask
when designing such systems is not:
"/f something will go wrong, but
when
it will go wrong?"
Some Examples
Now, ambitious systems that fail are
really much more common than we
may realize. In fact in some circum-
stances we strive for them, revelling
in the excitement of the unex-
pected. For example, let me remind
you of our national sport of foot-
ball. The whole object of the game
is for each team to play at the limit
of its abilities. Besides the sheer
physical skill required, one has the
strategic intricacies, the ability to
audibilize, and the quickness to
react to the unexpected--all a deep
part of the game. Of course, occa-
sionally one team approaches per-
fection, all the plays work, and the
game becomes dull.
Another example of a system
that is too ambitious for perfection
is military warfare. The same ele-
ments are there with opposing sides
having to constantly improvise and
deal with the unexpected. In fact
we get from the military that won-
derful acronym, SNAFU, which is
politely translated as "situation nor-
mal, all fouled up." And if any of
you are still doubtful, consider how
rapidly the phrases "precision
bombing" and "surgical strikes" are
replaced by "the fog of war" and
"casualties from friendly fire" as
soon as hostilities begin.
On a somewhat more whimsical
note, let me offer driving in Boston
as an example of systems that
will
fail. Automobile traffic is an excel-
lent case of distributed control with
a common set of protocols called
traffic regulations. The Boston area
is notorious for the free interpreta-
tions drivers make of these pesky
regulations, and perhaps the epit-
ome of it occurs in the arena of the
traffic rotary. A case can be made
for rotaries. They are efficient.
There is no need to wait for slug-
gish traffic signals. They are direct.
And they offer great opportunities
for creative improvisation, thereby
adding zest to the sport of driving.
One of the most effective strate-
gies is for a driver approaching a
rotary to rigidly fix his or her head,
staring forward, of course, secretly
using peripheral vision to the limit.
It is even more effective if the
driver on entering the rotary,
speeds up, and some drivers embel-
lish this last step by adopting a look
of maniacal glee. The effect is, of
course, one of intimidation, and a
pecking order quickly develops.
The only reason there are not
more accidents is that most drivers
have a second component to the
strategy, namely, they assume
everyone else may be crazy--they
are often correct--and every driver
is really prepared to stop with
inches to spare. Again we see an
example of a system where ambi-
tious tactics and prudent caution
lead to an effective solution.
So far, the examples I have given
may suggest that failures of ambi-
tious systems come from the human
element and that at least the techni-
cal parts of the system can be built
correctly. In particular, turning to
computer systems, it is only a mat-
ter of getting the code debugged.
Some assume rigorous testing will
do the job. Some put their hopes in
proving program correctness. But
unfortunately, there are many cases
for which none of these techniques
will always work [1]. Let me offer a
modest example illustrated in Fig-
ure 1.
Consider the case of an elaborate
numerical calculation with a vari-
able, f, representing some physical
value, being calculated for a set of
points over a range of a parameter,
t. Now the property of physical
variables is that they normally do
not exhibit abrupt changes or dis-
continuities.
So what has happened here? If
we look at the expression for f, we
see it is the result of a constant, k,
added to the product of two other
functions, g and h. Looking further,
we see that the function g has a be-
havior that is exponentially increas-
ing with t. The function h, on the
other hand, is exponentially de-
creasing with t. The resultant prod-
uct of g and h is almost constant
with increasing t until an abrupt
jump occurs and the curve for f
goes flat.
What has gone wrong? The an-
swer is that there has been floating-
point underflow at the critical point
in the curve, i.e., the representation
of the negative exponent has ex-
ceeded the field size in the floating-
COMMUNICATIONS OF THE ACM/September
1991/Vol.34, No.9 7
3
I
A Subtle Bug
Where
f(t)=k+ g(t).h(t)
g(t)-exp(at)
(a>O)
h(t)-exp(-bt)
(b>O)
t -.--I1,,.-
•.. Why Mishaps?
iii
Performance
100
10
MIPS
1
:IGURE
qGURE !
0.1
1950 1970 1990
Year
point representation for this partic-
ular computer, and the hardware
has automatically set the value for
the function h to zero. Often this is
reasonable since small numbers are
correctly approximated by zero--
but not in this case, where our re-
sults are grossly wrong. Worse yet,
since the computation off might be
internal, it is easy to imagine that
the failure shown here would not
be noticed.
Because correctly handling the
pathology that this example repre-
sents is an extra engineering
bother, it should not be surprising
that the problem of underflow is
frequently ignored. But the larger
lesson to be learned from this ex-
ample is that subtle mistakes are
very difficult to avoid and to some
extent are inevitable.
I encountered my next example
when I was a graduate student pro-
gramming on the pioneering
Whirlwind computer. One night
while awaiting my turn to use it, the
graduate student before me began
complaining of how "tough" some
of his calculations were. He said he
was computing the vibrational fre-
quencies of a particular wing struc-
ture for a series of cases. In fact, his
equations were cubics, and he was
using the iterative Newton-Raph-
son method. For reasons he did not
understand, his method was find-
ing one of the roots, but not "con-
verging" for the others. He was try-
ing to fix this situation by changing
his program so that when he en-
countered one of these tough roots,
the program would abandon the
iteration after a fixed number of
tries.
Now there were several things
wrong: First, the coefficients to his
cubic equations were based on ex-
Debugging the Code
Nonconverglng Iteratlve Method
Caused by Poor Root Value
:IGURE |
Performance of a Top-of-the-Line
Computer by Decade
74
September 1991/Vol.34, No.9/COMMUNIOATIONS OF THE AGM
perimental data and some of his
points were simply bad. Therefore,
as Figure 2 illustrates, he only had
one real root and a pair of im-
aginaries. Thus his iterative
method could never converge for
the second and third roots and the
value of his first root was pure gar-
bage. Second, cubic equations have
an exact analytic closed form solu-
tion so that it was entirely unneces-
sary to use an iterative method.
And third, based on his incomplete
model and understanding of what
was happening, he exercised very
poor judgment in patching his pro-
gram to ignore values that were
seemingly difficult to compute.
Ambitious System Properties
Let me turn next to some of the
general properties of ambitious sys-
tems. First, they are often vast and
have significant organizational
structures going beyond that of
simple replication. Second, they are
frequently complicated or elaborate
and are too much for even a small
group to develop. Third, if they
really are ambitious, they are push-
ing the envelope of what people
know how to do, and as a result
there is always a level of uncertainty
about when completion is possible.
Because one has to be an optimist to
begin an ambitious project, it is not
surprising that underestimation of
completion time is the norm.
Fourth, ambitious systems when
they work, often break new
ground, offer new services and
soon become indispensable. Finally,
it is often the case that ambitious
systems by virtue of having opened
up a new domain of usage, invite a
flood of improvements and
changes.
Now one could argue that ambi-
tious systems are really only diffi-
cult the first time or two. It is really
only a matter of learning how to do
it. Once one has, then one simply
draws up the appropriate PERT
charts, hires good managers, en-
sures an adequate budget and gets
on with it. Perhaps there are some
in3tances where this works, but at
least in the area of computer sys-
tems, there is a fundamental reason
it does not.
A key reason we cannot seem to
get ambitious systems right is
change. The computer field is in-
toxicated with change. We have
seen galloping growth over a pe-
riod of four decades and it still does
not seem to be slowing down. The
field is not mature yet and already
it accounts for a significant percent-
age of the Gross National Product
both directly and indirectly. More
importantly the computer revolu-
tion-this second industrial revolu-
tion-has changed our life-styles
and allowed the growth of countless
new application areas. And all this
change and growth not only has
changed the world we live in, but
has raised our expectations, spur-
ring on increasingly ambitious sys-
tems in such diverse areas as airline
reservations, banking, credit cards,
and air traffic control to name only
a few.
Behind the incredible growth of
the computer industry is, of course,
the equally mind-boggling change
that has occurred in the raw perfor-
mance of digital logic. Figure 3,
which is not precise and which
many of you have seen before in
some form, gives the performance
of a top-of-the-line computer by
decade. The ordinate in MIPS is
logarithmic as you can see. In par-
ticular in the last decade, the graph
becomes problem dependent so
that the upper right-hand end of
the line should break up into some
sort of whiskers as more and more
computers are tailored for special
applications and for parallelism.
Complicating matters too is that
parallelism is not a solution for
every problem. Certain calculations
that are intrinsically serial, such as
rocket trajectories, derive very lim-
ited benefit from parallel comput-
ers. And one of course is reminded
of the old joke about the Army way
of speeding up pregnancy by hav-
ing nine women spend one month
at the task.
As Figure 4 makes clear, it is not
just performance that has fueled
growth but rather cost/perfor-
mance, or simply put, favorable
economics. The graph is an over-
simplification, but represents the
cost for a given performance com-
puter model over the last four dec-
ades. Again the ordinate is logarith-
mic, going from 10 million dollars
in 1950 down to one thousand dol-
lars in 1990. As we approach the
present, corresponding to a per-
sonal computer, the graph really
should become more complicated
since one consequence of comput-
ers becoming super-cheap is that
increasingly, they are being embed-
ded in other equipment. The mod-
ern automobile is but one example.
And it remains
to be seen
how general-
purpose the
current wave
of palm-sized
computers
will be with
their stylus
inputs.
Further, when we look at a pho-
tograph taken around 1960 of a
"machine room" staffed with one
lone operator, we are reminded of
the fantastic changes that have oc-
curred in computer technology.
The boxes are huge, shower-stall-
sized, and the overall impression is
of some small factory. You were
supposed to be impressed and the
operator was expected to maintain
decorum by wearing a necktie. And
if he did not, at least you could be
sure an IBM maintenance engineer
would.
Another reminder of the im-
mense technological change which
has occurred is in the physical di-
mensions of the main memories of
computers. For example, if one
looks at old photographs taken in
the mid-1950s of core memory sys-
COMMUNICATIONS OF THE ACM/September i991/Vo1.34, No.9 7S
Cost/Performance
$10M
100K
1K
1950 1970 1990
Year
:IGURE 4
COSt for Given-Performance Computer Model over Four Decades
CTSS: Architecture
P1
iii!iii!i!i!i!iii!!!iii i! iiiiiiiiiiiiiiiiiiiiiiiiiiiiiii!i!i!iii!i!i!i!ii !
P2
I
iiiiiiiiiiiii21~iiiiii::i::i::i::i::i::i::i::i::i::i::i::i::i::i::2::i::i]iiiil
Memory
A Simplified View
=IGURE !
Input/Output of User Programs
tems, one typically sees a core mem-
ory plane roughly the size of a ten-
nis racquet head which could hold
about 1,000 bits of information.
Contrast that with today's 4megabit
memory chips that are smaller than
one's thumb.
The basis of the Award today is
largely for my work on two pio-
neering time-sharing systems,
CTSS [5, 6] and Multics [7, 9]. In-
deed, it is from my involvement
with those two systems that I gained
the system-building perspective I
am offering. It therefore seems
appropriate to take a brief retro-
spective look at these two systems as
examples of ambitious systems and
to explore the reasons why the
complexity of the tasks involved
made it almost impossible to build
the systems correctly the first time
[2].
CTSS, The Compatible Time-
Sharing System
Looking first at CTSS, let us re-
member the dark ages that existed
then. This was the early 1960s. The
computers of the day were big and
expensive, and the administrators
of computing centers felt obliged to
husband the precious resource.
Users, i.e., programmers, were
expected to submit a computing job
as a deck of punched cards. These
were then combined into a batch
with other jobs onto a magnetic
tape and the tape was processed by
the computer operating system. It
had all the glamour and excitement
of dropping one's clothes off at a
laundromat.
The problem was that even for a
trivial input typing mistake, the job
would be aborted. Time-sharing, as
most of you know, was the solution
to the problem of not being able to
interact with computers. The gen-
eral vision of modern time-sharing
was primarily spelled out by John
McCarthy, who I am pleased to
note is a featured speaker at this
conference. In England, Christo-
pher Strachey independently came
up with a limited kind of interactive
computing, but it was aimed mostly
at debugging. Soon there were
many groups around the country
developing various forms of inter-
active computing, but in almost all
cases, the resulting systems had sig-
nificant limitations.
It was in this context that my own
group developed our version of the
time-sharing vision. We called it
The Compatible Time-Sharing Sys-
tem, or CTSS for short. Our initial
aspirations were modest. First, the
system was meant to be a demon-
stration prototype before more
ambitious designs being attempted
by others could be implemented.
Second, it was intended to handle
general-purpose programming.
And third, it was meant to make it
possible to run most of the large
body of software that had been de-
veloped over the years in the batch-
processing environment. Hence the
name.
The basic scheme used to run
7G
September 1991/Vol.34, No.9/COMMUNICATIONS OF THE ACM
CTSS was simple. The supervisor
program, which was always in main
memory, would commutate among
the user programs, running each in
turn for a brief interval with the
help of an interval timer. As Figure
5 indicates, user programs could do
input/output with the typewriter-
like terminals and with the disk
storage unit as well.
But the diagram is oversimpli-
fied. The key difficulty was that
main memory was in short supply
and not all the programs of the ac-
tive users could remain in memory
at once. Thus the supervisor pro-
gram not only had to move pro-
grams to and from the disk storage
unit, but it also had to act as an in-
termediary for all I/O initiated by
user programs. Thus all the I/O
lines should only point to the su-
pervisor program.
As a further complication, the
supervisor program had to prevent
user programs from trampling over
one another. To do this required
special hardware modifications to
the processor such that there were
memory bound registers that could
only be set by the supervisor. Nev-
ertheless, despite all the complica-
tions, the simplicity of the initial
supervisor program allowed it to
occupy about 22 Kbytes of
storageless storage than required
for the text of this talk!
Most of the battles of creating
CTSS involved solving problems
which at the time did not have stan-
dard solutions. For example: There
were no standard terminals. There
were no simple modems. I/O to the
computer was by word and not by
character, and worse yet, did not
accommodate lower case letters.
The computers of the day had nei-
ther interrupt timers nor calendar
clocks. There was no way to prevent
user programs from issuing raw
I/O instructions at random. There
was no memory protection scheme.
And, there was no easy way to store
large amounts of data with rela-
tively rapid random access.
The overall result of building
CTSS was to change the style of
computing, but there were several
effects that seem worth noting. One
of the most important was that we
discovered that writing interactive
software was quite different from
software for batch operation and
even today, in this era of personal
computers, the evolution of inter-
active interfaces continues.
In retrospect, several design de-
cisions contributed to the success of
CTSS, but two were key. First, we
could do general-purpose pro-
gramming and, in particular, de-
velop new supervisor software
using the system itself. Second, by
making the system able to accom-
modate older batch code, we inher-
ited a wealth of older software
ready-to-go.
One important consequence of
developing CTSS was that for the
first time, users had persistent on-
line storage of programs and data.
Suddenly the issues of privacy, pro-
tection and backup of information
had to be faced. Another byproduct
of the development was that be-
cause we operated terminals via
modems, remote operation became
the norm. Also, the new-found
freedom of keeping information
on-line in the central file system
suddenly made it especially conve-
nient for users to share and ex-
change information among them-
selves.
And there were surprises too. To
our dismay, users who had been
enduring several-hour waits be-
tween jobs run under batch pro-
cessing were suddenly restless
when response times were more
than a second. Moreover, many of
the simplifying assumptions that
had allowed CTSS to be built so
simply, such as a one-level file sys-
tem, suddenly began to chafe. It
seemed like the more we did, the
more users wanted.
There are two other observations
that can be made about the CTSS
system. First, it lasted far longer
than we expected. Although CTSS
had been demonstrated in primi-
tive form in November 1961, it was
not until 1963 that it came into wide
were two copies of the system hard-
ware, but by 1973 the last copy was
turned off and scrapped primarily
because the maintenance costs of
the IBM 7094 hardware had be-
come prohibitively expensive, and
up to the bitter end, there were
users desperately trying to get in a
few last hours of use.
Second, the then-new transistors
and large random-access disk files
were absolutely critical to the suc-
cess of time-sharing. The previous
generation of vacuum tubes was
simply too unreliable for sustained
real-time operation and, of course,
large disk files were crucial for the
central storage of user programs
and data.
A Mishap
My central theme is to try to con-
vince you that
when
you have a
multitude of
novel issues
to contend
with while
building a
system,
mistakes are
inevitable.
And indeed, we had a beauty while
using CTSS. Let me describe it:
What happened was that one af-
ternoon at Project MAC, where
CTSS was being used as the main
time-sharing workhorse, any user
who logged in, found that instead
of the usual message-of-the-day
typing out on his or her terminal,
he had the entire file of user pass-
words. This went on for 15 or 20
minutes, until one particularly con-
scientious user called the system
administrator and began the con-
versation with "Did you know that
use as the vehicle of a Project MAC . . . ?" Needless to say, there was
Summer Study. For a time there general consternation with this co-
COMMUNICATIONS OF THE
ACM/Septcmber 1991/%1.34, No.9 1~7
lossal breach of security, the system
was hastily shut down and the next
twelve hours were spent heroically
changing everyone's password. The
question was how could this have
happened? Let me explain.
To simplify the organization of
the initial CTSS system, a design
decision had been made to have
each user at a terminal associated
with his or her own directory of
files. Moreover, the system itself
was organized as a kind of quasi-
proceeded to cajole me into letting
the system directory be an excep-
tion so that more than one person
at a time could be logged into it.
They assured me that they would
be careful to not make mistakes.
But of course a mistake was
made. A software design decision in
the standard system text editor was
overlooked. It was assumed that the
editor would only be used by one
user at a time working in one direc-
tory so that a temporary file could
CTSS: A Mishap
System Password File became the Message-of-the-Day
iiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii . ............. .....
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
iiiiii)iiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii)iiiii;ii}iiiiii
!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
:':?:'T"T':'':':':':':':':'"'T":?':?"
!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:!:
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
:::::::::::::::::::::::':::::':::::::::::::: :::::::::::::::::::::
iiiiiiiiiiiiii~iii~i!i!iiiiiiiiiii!i~iii~i~iiiiiii~i;ii~!!!i!!~!!i .........................
:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i:i "--... l!iiiiiiiiiiiii ! ii o' a!!iii i iiiiiii l
iiiiiiiiiiiiiii?iiiii?iiiiiiiiiiiiiiiiiiiii:iiiiiiiiiiiiiiiiiiiii?
!!!!!!!!!!!!s!!!!!!!!i!!!i!i!ii!!i!!!!!!i!!ii!!ii!i!i!i!s!i!i!!!ii
:+:,:,:+:.:+:.:+:.:.:.:.:.:.:.:.:.:.:.:.:.:.:.:.:.:.:+:.
:i:i:i:i:i:!:i:i:i:!:i:i:bi:i:i:i:bbi:~:!:i:!:!:!:i:!:!:!
:,:+:+:+:+:+:.:.:.:.:+:.:,:+:+:.:+:+:.:.:+:.
'IGURE |
CTSS
Is full of Surprises
user with its own directory that in-
cluded a large number of support-
ing applications and files, including
the message-of-the day and the
password file. So far, so good. Nor-
mally a single-system programmer
could login to the system directory
and make any necessary changes.
But the number of system pro-
grammers had grown to about a
dozen in number, and, further, the
system by then was being operated
almost continuously so that the
need to do live maintenance of the
system files became essential. Not
surprisingly, the system program-
mers saw the one-user-to-a-direc-
tory restriction as a big bottleneck
for themselves. They thereupon
have the same name for all instan-
tiations of the editor. But with two
system programmers editing at the
same time in the system directory,
the editor temporary files became
swapped and the disaster occurred.
One can draw two lessons from
this: First, design bugs are often
subtle and occur by evolution with
early assumptions being forgotten
as new features or uses are added to
systems. Second, even skilled pro-
grammers make mistakes.
Multlcs
Let me turn now to the develop-
ment of Muhics [12]. I will be brief
since the system has been docu-
mented well and there have already
been two retrospective papers writ-
ten [3, 4]. The Muhics system was
meant to do time-sharing "right"
and replace the previous ad hoc
systems such as CTSS. It started as
a cooperative effort among Project
MAC of MIT, the Bell Telephone
Laboratories, and the Computer
Department of General Electric,
later acquired by Honeywell. In our
expansiveness of purpose we took
on a long list of innovations.
Among the most important ones
were the following: First, we intro-
duced into the processor hardware
the mechanisms for paging and
segmentation along with a careful
scheme for access control. Second,
we introduced an idea for rings of
protection around the supervisor
software. Third, we planned from
the start that the system would be
composed of interchangeable mul-
tiple processors, memory modules,
and so forth. And fourth, we made
the decision to implement nearly all
of the system in the newly defined
compiler language, PL/I.
Let me share a few of my obser-
vations about the Muhics experi-
ence. The novel hardware we had
commissioned meant that the sys-
tem had to be built from the
ground up so that we had an im-
mense task on our hands.
The decision to use a compiler to
implement the system software was
a good one, but what we did not
appreciate was that new language
PL/I presented us with two big dif-
ficulties: First, the language had
constructs in it which were intrinsi-
cally complicated, and it required a
learning period on the part of sys-
tem programmers to learn to avoid
them. Second, no one knew how to
do a good job of implementing the
compiler. Eventually we overcame
these difficulties but it took pre-
cious time.
That Muhics succeeded is re-
markable, for it was the result of a
cooperative effort of three highly
independent organizations and had
no administrative head. This meant
decisions were made by persuasion
and consensus. Consequently, it
was difficult to reject weak ideas
until considerable time and effort
had been spent on them.
The Muhics system did turn into
78
September 1991/Vo1.34, No.9/COMMUNICATIONS
OF THE ACM
a commercial product. Some of its
major strengths were the virtual
memory system, the file system, the
attention to security, the ability to
do online reconfiguration, and the
information backup system for
the
file system.
And, as was also true with CTSS,
many of the alumni of the Multics
development have gone on to play
important roles in the computing
field [11].
A few more observations can be
made about the ambitious Multics
experience. In particular, we were
misled by our earlier successes with
previous systems such as CTSS,
where we were able to build them
"brick-by-brick," incrementally add-
ing ideas to a large base of already
working software.
We also were embarrassed by our
inability to set and meet accurate
schedules for completion of the dif-
ferent phases of the project. In ret-
rospect, we should not have been,
for we had never done anything
like it before. However in many
cases, our estimations should have
been called guesses.
The Unix system [15] was a reac-
tion to Multics. Even the name was
a joke. Ken Thompson was part of
the Bell Laboratories' Multics ef-
fort, and, frustrated with the at-
tempts to bring a large system de-
velopment under control, decided
to start over. His strategy was clear--
Start small and build up the ideas
one by one as he saw how to imple-
ment them well. As we all know,
Unix has evolved and become im-
mensely successful as the system of
choice for workstations. Still there
are aspects of Multics that have
never been replicated in Unix.
As a commercial product of
Honeywell and Bull, Multics devel-
oped a loyal following. At the peak
there were about 77 sites worldwide
and even today many of the sites
tenaciously continue for want of an
alternative.
Sources of Complexity
The general problem with ambi-
tious systems is complexity. Let me
next try to abstract some of the
major causes. The most obvious
complexity problems arise from
scale. In particular, the larger the
personnel required, the more levels
of management there will be. We
can see the problem even if we use
simplistic calculations. Thus if we
assume a fixed supervision ratio,
for example six, the levels of man-
agement will grow as the logarithm
of the personnel. The difficulty is
that with more layers of manage-
ment, the top-most layers become
out of touch with the relevant bot-
tom issues and the likelihood of
random serendipitous communica-
tion decreases.
Another problem of organiza-
tions is that subordinates hate to
report bad news, sometimes for
fear of "being shot as the messen-
ger" and at other times because
they may have a different set of
goals than the upper management.
And finally, large projects en-
courage specialization so that few
team members understand all of
the project. Misunderstandings and
miscommunication begin, and soon
a significant part of the project re-
sources are spent fighting internal
confusion. And, of course, mistakes
occur.
My next category of complexity
arises because of new design do-
mains. The most vivid examples
come from the 'world of physical
systems, but software too is subject
to the same problems, albeit often
in more subtle ways.
Consider the destruction of the
Tacoma Narrows Bridge, in Wash-
ington State, on November 7, 1940.
The bridge bad been proudly
opened about four months earlier.
Many of you have probably seen
the amateur movie that was fortu-
nately made of the collapse. What
happened is that a strong but not
unusual crosswind blew that day.
Soon the roadbed, suspended by
cables from the main span, began to
vibrate like a reed, and the more it
flexed, the better cross section it
presented to the wind. The result
was that the bridge tore itself apart
as the oscillations became large and
violent. What we had was a case of a
new design domain where the clas-
sic bridge builder, concerned with
gravity-loaded structures, had en-
tered into the realm of aeronautics.
The result was a major mistake.
Next, let us look at the complexi-
ties that arise from human usage of
computer systems. In using online
systems that allow the sharing or
exchanging of information--and
here networked workstations
clearly fall in this class--one is
faced with a dilemma: If one places
total trust in all other users, one is
vulnerable to the antisocial behav-
ior of any malicious user--consider
the case of viruses. But
if one tries
to
be totally
reclusive and
isolated, one
is not only
bored, but
one ' s
information
universe
will cease
to
grow
and be
enhanced
by inter-
action with
others.
The result is that
most of us operate in a complicated
trade-off zone with various ar-
rangements of trust and security
mechanisms. Even such simple
ideas as passwords are often a prob-
lem. They are a nuisance to re-
member, they can easily be com-
promised inadvertently, and they
cannot be selectively revoked if
shared. Privacy and security issues
COMMUNICATIONS
OF THE
ACM/September 1991/Vol.34, No.9 79
are particularly difficult to deal
with since responsibilities are often
split among users, managers, and
vendors.
Wor
s e
yet, there
is no way
to simply
"look" at a
system and
determine
what the
privacy
and security
implications
are. It is
no wonder
mistakes
occur all
the time
in this area.
One of the consequences of
using computer systems is that in-
creasingly information is being kept
on-line in central storage devices.
Computer storage devices have
become remarkably reliable--
except when they break--and that
is the rub. Even the most experi-
enced computer user can find him-
or herself lulled into a false sense of
security by the almost perfect oper-
ation of today's devices. The prob-
lem is compounded by the attitude
of vendors, not unlike the initial
attitude of the automobile industry
toward safety, where inevitable disk
failure is treated as a negative issue
that dampens sales.
What is needed is constant vigi-
lance against a long list of "what
ifs": hardware failure, human slips,
vandalism, theft, fire, earthquakes,
long-term media failure, and even
the loss of institutional memories
concerning recovery procedures.
And as long as some individuals
have to "learn the hard way," mis-
takes will continue to be made.
A further complication in dis-
cussing risk or reliability is that
there is not a good language with
which to carry on a dialog. Statistics
are as often misapplied as they are
misunderstood. We also get absurd
absolutes such as "the Strategic
Defense Initiative will produce a
perfect unsaturatable shield against
nuclear attack" [14] or "it is impos-
sible for the reactor to overheat."
The problem is that we always have
had risks in our lives, we never have
been very good at discussing them,
and with computers we now have a
lot of new sources.
Another source of complexity
arises with rapid change, change
which is often driven by technology
improvements. A result is that
changes in procedures or usage
occur and new vulnerabilities can
arise. For example, in the area of
telephone networks, the economies
and efficiencies of fiber optic cables
compared to copper wire are rap-
idly causing major upgrades and
replacements in the national tele-
phone plant. Because one fiber
cable can carry at a reasonable cost
the equivalent traffic of thousands
of copper wires, fiber is quickly
replacing copper. As a result, a
transformation is likely to occur
where network links become spar-
ser over a given area and multiply
interconnected nodes become less
connected.
The difficulty is that there is re-
duced redundancy and a much
higher vulnerability to isolated acci-
dents. In the Chicago area not long
ago there was a fire at a fiber optics
switching center that caused a loss
of service to a huge number of cus-
tomers for several weeks. More re-
cently, in New York City there was a
shutdown of the financial ex-
changes for several hours because
of a single mishap with a backhoe in
New Jersey. Obviously in both in-
stances, efficiency had gotten ahead
of robustness.
The last source of complexity
that I will single out arises from the
frailty of human users when forced
to deal with the multiplicity of tech-
nologies in modern life. In a little
more than a century, there has
been an awesome progression of
technological changes from tele-
phones and electricity, through
automobiles, movies and radio--I
will not even try to complete the list
since we all know it well. The over-
all consequence has been to pro-
duce vast changes in our life-styles,
and we see these changes even hap-
pening today. Consider the changes
in the television editing styles that
have occurred over a few decades,
the impact of viewgraph overhead
projectors on college classrooms,
and the way we now do our banking
with automatic teller machines.
And the progression of life-style
changes continues at a seemingly
more rapid pace with word process-
ing, answering machines, facsimile
machines, and electronic mail.
One consequence of the many
life-style changes is that some indi-
viduals feel stressed and overstimu-
lated by the plethora of inputs. The
natural defense is to increasingly
depend on others to act as informa-
tion filters. But the combination of
stressful life-styles and insu'lation
from original data will inevitably
lead to more confusion and mis-
takes.
Conclusions
Most of this talk has been directed
toward trying to persuade you that
failures in complex, ambitious sys-
tems are inevitable. However, I
would be remiss if I did not address
ways to resolve the problem. Un-
fortunately, the list I can offer is
rather short but worthy of brief
review.
First, it is important to emphasize
the value of simplicity and ele-
gance, for complexity has a way of
compounding difficulties and as we
have seen, creating mistakes. My
definition of elegance is the
achievement of a given functional-
ity with a minimum of mechanism
and a maximum of clarity.
80 September 1991/%7ol.34, No.9/COMMUNICATIONS OF THE ACM
Second, the value of metaphors
should not be underestimated.
Metaphors have the virtue of an
expected behavior that is under-
stood by all. Unnecessary commu-
nication and misunderstandings
are reduced. Learning and educa-
tion are quicker. In effect, meta-
phors are a way of internalizing and
abstracting concepts allowing one's
thinking to be on a higher plane
and low-level mistakes to be
avoided.
Third, use of constrained lan-
guages for design or synthesis is a
powerful methodology. By not al-
lowing a programmer or designer
to express irrelevant ideas, the
domain of possible errors becomes
far more limited.
Fourth, one must try to antici-
pate both errors of human usage
and of hardware failure and prop-
erly develop the necessary contin-
gency paths. This process of play-
ing "what if" is not as easy as it may
sound, since the need to attach like-
lihoods of occurrence to events and
to address issues of the indepen-
dence of failures is implicit.
Fifth, it should be assumed in the
design of a system, that it will have
to be repaired or modified. The
overall effect will be a much more
robust system, where there is a high
degree of functional modularity
and structure, and repairs can be
made easily.
Sixth, and last, on a large project,
one of the best investments that can
be made is the cross edtccation of
the team so that nearly everyone
knows more than he or she needs to
know. Clearly, with educational
redundancy, the team is more resil-
ient to unexpected tragedies or
departures. But in addition, the
increased awareness of team mem-
bers can help catch global or sys-
temic mistakes early. It really is a
case of "more heads are better than
one."
Finally, I have touched on many
different themes in this talk but I
will single out three: First, the evo-
lution of technology supports a rich
future for ambitious visions and
dreams that will inevitably involve
complex systems. Second, one must
always try to learn from past mis-
takes, but at the same time be alert
to the possibility that new circum-
stances require new solutions. And
third, one must remember that
ambitious systems demand a defen-
sive philosophy of design and im-
plementation. In other words,
"Don't wonder/f some mishap may
happen, but rather ask
what
one will
do about it when it does occur." r'.l
References
1. Brooks, F.P., Jr. No silver bullet.
IEEE Comput.
(Apr. 1987), 10-19.
2. Corbat6, F.J. Sensitive issues in the
design of multi-use systems. Un-
published lecture transcription of
Feb. 1968, Project MAC Memo
M-383.
3. Corbat6, F.J., and Clingen, C.T. A
managerial view of the Muhics sys-
tem development. In
Research Direc-
tions in Software Technology,
P. Weg-
ner, Ed., M.I.T. Press, 1979. (Also
published in
Tutorial: Software Man-
agement,
D.J. Reifer, Ed., IEEE
Computer Society Press, 1979; Sec-
ond Ed,, 1981; Third Ed., 1986.)
4. Corbat6, F.J., Clingen, C.T., and
Saltzer, J.H. Multics: The first
seven years. In
Proceedings of the
SJCC
(May 1972), pp. 571-583.
5. Corbat6, F.J., Daggett, M.M., and
Daley, R.C. An experimental time-
sharing system. In
Proceedings of the
Spring Joint Computer Conference
(May 1962).
6. Corbat6, F.J., Daggett, M.M., Daley,
R.C., Creasy, R.J., Hellwig, J.D.,
Orenstein, R.H., and Horn, L.K.
The Compatible Time-Sharing System:
A Programmer's Guide.
M.I.T. Press,
June 1963.
7. Corbat6, F.J., and Vyssotsky, V.A.
Introduction and overview of the
Multics system. In
Proceedings FJCC
(I965).
8. Daley, R.C. and Neumann, P.G. A
general-purpose file system for sec-
ondary storage. In
Proceedings FJCC
(1965).
9. David, E.E., Jr. and Fano, R.M.
Some thoughts about the social
implications of accessible comput-
ing. In
Proceedings FJCC
(1965).
10. Glaser, E.L., Couleur, J.F. and Ol-
iver, G.A. System design of a com-
puter for time-sharing applications.
In
Proceedings FJCC
(1965).
11. Neumann, P,G., a Multics veteran,
has become a major contributor to
the literature of computer-related
risks. He is the editor of the widely-
read network magazine "Risks-
Forum," writes the "Inside Risks"
column for the CACM, and period-
ically creates digests in the ACM
Software Engineering Notes.
12. Organick, E.I.
The Multics System: An
Examination of its Structure.
MIT
Press, 1972.
13. Ossanna, J.F., Mikus, L. and Dun-
ten, S.D. Communications and
input-output switching in a Multi-
plex computing system. In
Proceed-
ings FJCC
(1965).
14. Parnas, D.L. Software aspects of
strategic defense systems.
Am. Sci.
(Nov. 1985). An excellent critique
on the difficulties of producing
software for large-scale systems.
15. Ritchie, D.M. and Thompson, K.
The UNIX time-sharing system.
Commun, ACM 17,
7 (July 1974),
365-375.
16. Vyssotsky, V.A., and Corbat6, F.J.
Structure of the Multics Supervisor.
In
Proceedings FJCC,
1965.
CR Categories and Subject Descrip-
tors: C.2 [Computer Systems Organiza-
tion]:
Computer-Communication Net-
works; C.4
[Computer Systems
Organization]:
Performance of Sys-
tems; D.4 [Software]: Operating Sys-
tems; H.5 [Information Systems]: In-
formation Interfaces and Presentation;
K.2 [Computing Milieux]: History of
Computing
General Terms: Design
About the Author:
FERNANDO J. CORBATO
is Associate
Head of Computer Science and Engi-
neering at the Massachusetts Institute of
Technology.
Author's Present Address:
Computer Science and Engineering
Department, Room NE43-514, 545
Technology Square, Cambridge, MA
02139.
Permission to copy without fee all or part of
this material is granted provided that the
copies are not made or distributed for direct
commercial advantage, the ACM copyright
notice and the title of the publication and its
date appear, and notice is given that copying
is by permission of the Association for
Computing Machinery. To copy otherwise, or
to republish, requires a fee and/or specific
permission.
© ACM 0002-0782/91/0900-072 $1.50
COMMUNICATIONS OF THE ACM/September 1991/Vo1.34, No.9 81
There are a few reasons why the **Newton-Ralphson** method can fail to converge (though these are not really applicable to the situation mentioned by the author):
- Derivative may be zero at the root
- Function may fail to be continuously differentiable
- Choosing a bad starting point, i.e. one that lies outside the range of guaranteed convergence
### Why are rocket trajectories intrinsically serial?
Usually, problems that you can split into many smaller independent parts tend to be easily parallelizable. For instance, ray tracing (rendering a 3d scene) is easily parallelizable because each pixel represents a separate compute operation that can be executed independently.
For the trajectory of a rocket, you can’t split it into many different sections and compute them separately. The reason being that the later portions of the trajectory of the rocket depend on the earlier ones.
[Reminiscences on the history of time sharing](https://web.archive.org/web/20071020032705/http://www-formal.stanford.edu/jmc/history/timesharing/timesharing.html) is a wonderful article written by John McCarthy where he explains the early stages of time sharing
[Here](https://www.computerhistory.org/revolution/punched-cards/2/211/2253) is an entertaining short film made by Stanford students in the late 60s about the trials and tribulations of a college programmer condemned to use batch processing
[](https://www.computerhistory.org/revolution/punched-cards/2/211/2253)
Here is a photo of Corbató himself with MIT's IBM 7090 in 1961.

The [NBS DYSEAC](https://bit.ly/2lFxSa4 ) was the first computer to have an I/O interrupt.
This trend mostly continued until today:

To give you a sense of the price of a mainframe back in the 60s, the [IBM 7090](https://www.ibm.com/ibm/history/exhibits/mainframe/mainframe_PP7090.html), the computer used for CTSS, sold for \$2.9 million (equivalent to \$19 million today) or could be rented for \$63,500 a month (equivalent to \$421,000 today).

*IBM 7090*
### Floating Point Numbers
You can think of floating point numbers as being written in *scientific notation*. A floating point number has 3 parts:
-**sign**: indicates whether the number is positive or negative
-**significant**: The significant digits of the number
-**exponent**: indicates how large (or small) the number is
Example
Let’s say we wanted to store `2019` as a floating point number:
- Decimal Representation: `2019`
- Binary Representation: `11111100011`
- Scientific notation: $2.019 \times 10^{3}$
- Binary Scientific notation: $1.1111100011 \times 2^{10}$
- Double Precision Raw Binary:

As you can see in the raw binary, the exponent is stored as `10000001001`, which is `1033`: `10` (the actual binary exponent) + `1023` (the bias, which allows you to store the exponent as an unsigned integer). This means that the exponent range is `−1022` to `+1023` (exponents of `−1023` (all 0s) and `+1024` (all 1s) are reserved for special numbers.)
In this case, the floating point underflow mentioned in the paper would happen if you tried to save a floating point number with an exponent lower than `−1022`.
Completed in 1951, the *Whirlwind I* was a Cold War-era vacuum tube computer developed by the MIT Servomechanisms Laboratory for the U.S. Navy. Whirlwind began as a project for the US Navy to create a digital flight simulator for bomber crews. It occupied 3,300 square feet, had 512 bytes of main memory and could do 20,000 instructions per second. It featured several significant innovations: parallel digit processing, random-access and magnetic core memory, use video displays for output.
It is considered by many the first **real-time computer**, where the machine responds instantly, via video displays, to basic instructions from an operator.
[You can listen to a talk by Jay Forrester (head of the Whirlwind project) here.](https://www.youtube.com/watch?v=JZLpbhsE72I)

*Whirlwind computer room*
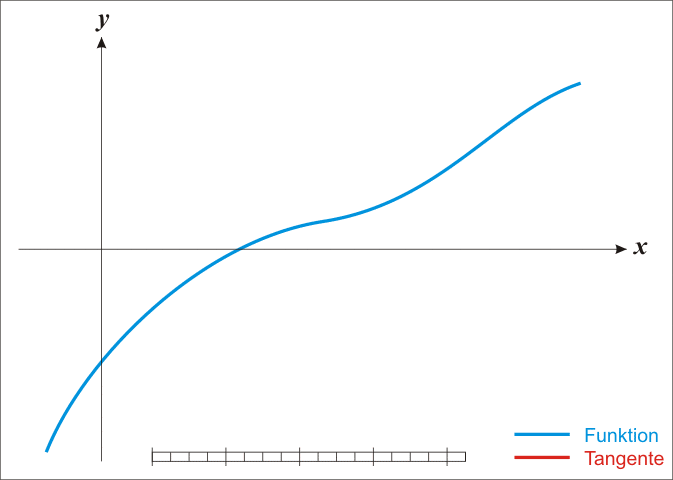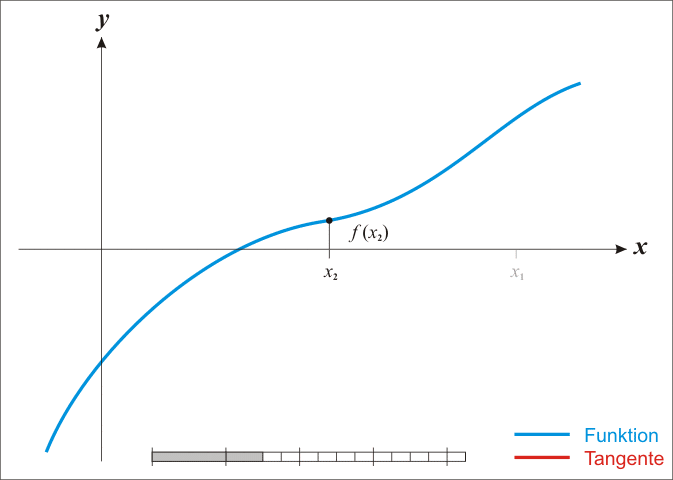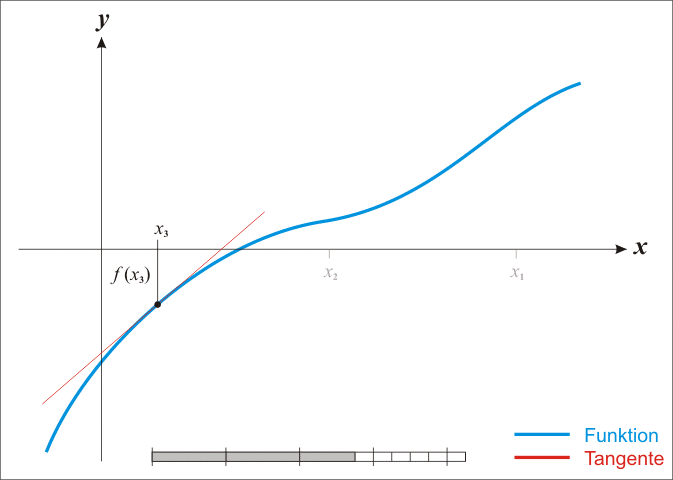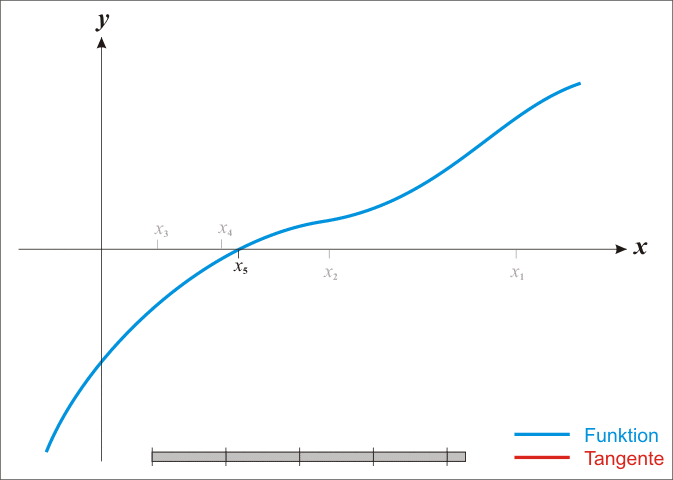
The **Newton-Ralphson** method is an iterative root-finding algorithm which produces successively better approximations to the zeroes of a real-valued function.
Here is a representation of a few iterations of the method: